The Power of Bitwise Operations in Swift

Reduce your space complexity

Image from Unsplash

Anyone who’s solved a sudoku knows that the solution is derived from the information you have, applying three rules to every following decision:

1. A number can appear only once in each 3x3 square
2. A number cannot appear twice on the same row
3. A number cannot appear twice on the same column

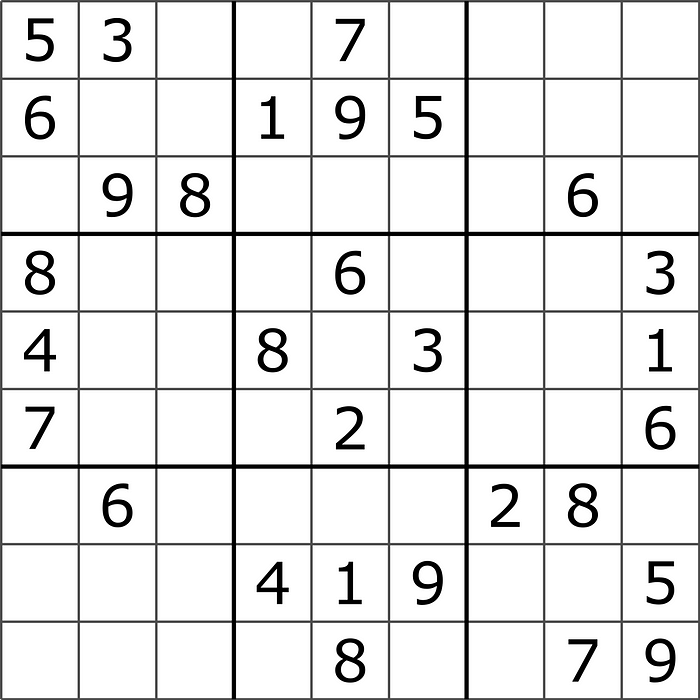
Following these rules, we can assert that in the first square of the sample sudoku, on the second row there is no chance there can be a 1, but certainly the second row will contain a 7. By exclusion you should be able to find a solution in which each 1x1 square contains a number between 1 and 9 and each 3x3 square, each row, and each column contains all numbers from 1 to 9.

Let’s say we want to write a program to test the current status of the sudoku and assert if it is a valid board, or if some of the rules are violated.

To write a sudoku checker, all we will have to do is fill a truth table for rows, one for columns, and one for squares. This truth table will tell us if the ith row/column/square already contains a number. If it does, the sudoku is not in a valid state.

Here’s a solution using the Swift programming language:

As input, we have a matrix of 9x9 of characters. Each character can either be a number between 1 and 9, or a dot, indicating that the spot is still free.

First, we construct our truth tables for our rules, then we iterate row by row, for each column traversing the whole board. If we find a number, we check if we already saw it before on the same row, or on the same column or in the same square. If we did, then we return false. If we didn’t we update our truth tables noting that we have seen this number at the row and col and square that we’re…